Yet Another Business Process Modeling Concept

Abstract

The task of business processes is important, relevant and occupies a worthy place in the field of business analysis. There is a large number of general purpose simulation systems, equipped with a detailed interface, statistical processing of simulation results and optimization of objects. The wide possibilities of objects of various types provided by such systems are accompanied by considerable difficulties in their mastering by users interested in business process but not being experts in the field of. In addition, manual construction of object simulation models in the environment can be very time-consuming. The article proposes an approach to the construction of a tool that provides automatic generation of executable simulation model of the business process, designed to run in the selected simulation system, but formed outside this environment. Such a tool can be a program-editor of a business process with the function of exporting a mathematical model of a business process to the executable file of its simulation model. The principal aspects of solving this problem in relation to simulation systems based on the formalisms of queuing networks and Petri nets are considered. A description is given of a functioning business process program-editor focused on using the GPSS World simulation system. The results of its application are demonstrated. The conclusion is made about the possibility and expediency of extending the proposed concept to other objects and simulation systems.

Keywords: Business processbusiness processautomated simulation model generating

Introduction

An objective assessment of various indicators of the business process is impossible without simulation. The choice of a business process format precedes the construction of its simulation model.

We will adhere to the following definition: a business process is an ordered set of activities, subordinated to the achievement of a single goal of completing a business process with a given result. Description and documentation of business processes is a necessary stage of implementation and successful functioning of the business process management system of the organization (Lapina et al., 2015; Yakimov, Kirpichnikov, Mokshin, Alyautdinova, & Pajgina, 2015; Zaharov, 2016). The presence of business processes that are properly documented provides a formal transition from a standardized description of the business process to its mathematical model (Artamonov, 2018).

Business analyst has a wide range of simulation systems that provide the construction and conduct experiments with the business process model. The process of building a model in a system environment can be tedious and require certain skills from the user. There is an objective contradiction: on the one hand, a business analyst is interested in obtaining an objective assessment of the time and cost indicators of the business process, and on the other hand, does not have the ability, and sometimes the desire, to master a complex system of simulation, which provides the construction of a simulation model of the business process.

The solution of this contradiction consists in the creation of a software product that provides an automated transition from a formal description of the object of a certain class to its simulation model intended for direct execution in a given simulation environment. This problem can be solved for a number of modern simulation systems (Gradišar & Mušič, 2012; Kanduč & Blaž, 2015).

To do this, certain requirements for the type and structure of the executable file of the simulation model must be met. These requirements, which are further described in the example of various simulation systems, can be defined as follows. The executable file of the simulation model must have the content and structure to be analyzed and decrypted. This condition is met by executable files of a significant number of simulation systems. In some cases, the model file is a text file (GPSS World (Safiullin, Devyatkov, & Zakirova, 2015) or C# file (Mobius (Keefe & Sanders, 2015), quite often it is an xml file (CPN Tools (Boubeta-Puig, Diaz, & Macia, 2019; Jensen & Kristensen, 2009), Anylogic (Nastyuk, Kulikova, Trubina, & Nazarov, 2017). In these and similar cases, the content of the executable file of the model can be analyzed and corrected. Thus, it becomes possible to automatically construct a simulation model intended to be launched in a given simulation environment, but formed outside this environment.

The feasibility of building such a bridge between the formal description of the business process and the modern simulation system is also due to the significant size and complex structure of real business processes.

Problem Statement

The task of building a simulation model of the business process is divided into the following stages.

1. To propose a general mathematical model of the business process, which allows further transition from the initial description of the business process to the format of its representation in a given simulation system.

2. To analyze the simulation systems for the possibility of external formation of the executable file of the model

3. To offer the rule of formation of the executable file of the chosen system of simulation modelling

Research Questions

We will be guided by the proposed model of the business process EXECUTOR in the form of a queuing network. To form an executable file of the simulation model, regardless of the formalism proposed by this modelling environment, it is necessary to solve the following tasks within this formalism.

1. To form the elements of the business process EXECUTOR structure - nodes of a queuing network.

2. To set claim routing between the nodes of a queuing network.

3. To set the duration distribution laws for the claim service in the nodes of a queuing network.

4. To set the parameters of the input claim flow of a queuing network.

5. To form an algorithm for transforming the parameters of the business process EXECUTOR into a formal model used by the selected simulation system. Next, it is necessary to provide an adequate representation of the business process model in the format of the simulation model executable file.

The last problem, the most difficult for any simulation systems is solved in different ways.

Purpose of the Study

The purpose of the study is to prove the feasibility of the proposed approach to business process modelling. For this purpose, analysis of simulation systems is performed for the possibility of external generation of the executable model file. A number of simulation systems based on various formalisms of modelling object representation are considered

Research Methods

Business process formal definition

1. The modern business process description standard BPMN (Yakimov, Kirpichnikov, Mokshin, Alyautdinova, & Pajgina, 2015) basically forms the structure of the business process with the help of task elements and logical functions XOR and AND. Up to the formal image of these elements, the activity set with an arbitrary order of their sequence can be represented by a probabilistic graph, a sample of which is shown on the top of Fig. 1 . The graph allowing parallelization of the business process and cyclic return to the already executed activities can be specified by the transmission matrix P of the following format. $P={\left\{p_{ij}\right\}}_{\begin{array}{c}i=\stackrel{-}{0,M}\\ j=\stackrel{-}{0,M}\end{array}}$ where M is the number of activities that are part of the business process, and $p_{ij}$ is the probability of transition to activity j after completion the activity i. Unlike the Markov matrix, the condition $\underset{j=0}{\overset{M}{\sum }}{p}_{ij}=1$ is not satisfied for all rows i of the matrix $P=\left\{p_{ij}\right\}$. If after the completion of activity i a simultaneous execution (parallelization) of several activities begins, for example, v and r, then $\underset{j=0}{\overset{M}{\sum }}{p}_{ij}=p_{iv}+p_{ir}=2$. Parallelization of works ultimately ends with their integration. Let us assume that only after the completion of activities v and r it is possible to start activity l. Then each of the elements $p_{vl}$ and $p_{vl}$ of the P matrix is supplied with a suffix #, meaning that the transition to activity l is allowed only after the completion of all activities with the suffix #, indicated in column l of the matrix P. The matrix P corresponding to the graph, Figure 01 , is shown in Figure 02 . In addition to the matrix P, the matrix $B=\left\{b_{i,r}\right\}$ for the executor assignment to activities is also given, where $b_{i,r}=1\vee 0$ depending on whether the activity i is assigned to the executor r. Adding data on the activity duration distributions and the input flow parameters, we can assume that the business process is specified. In fact, the formal business process EXECUTOR mathematical model is a nonlinear queuing network. Depending on the characteristics of the business process, this network can be homogeneous or heterogeneous, single-channel or multi-channel, open or closed.

See Full Size >

See Full Size >

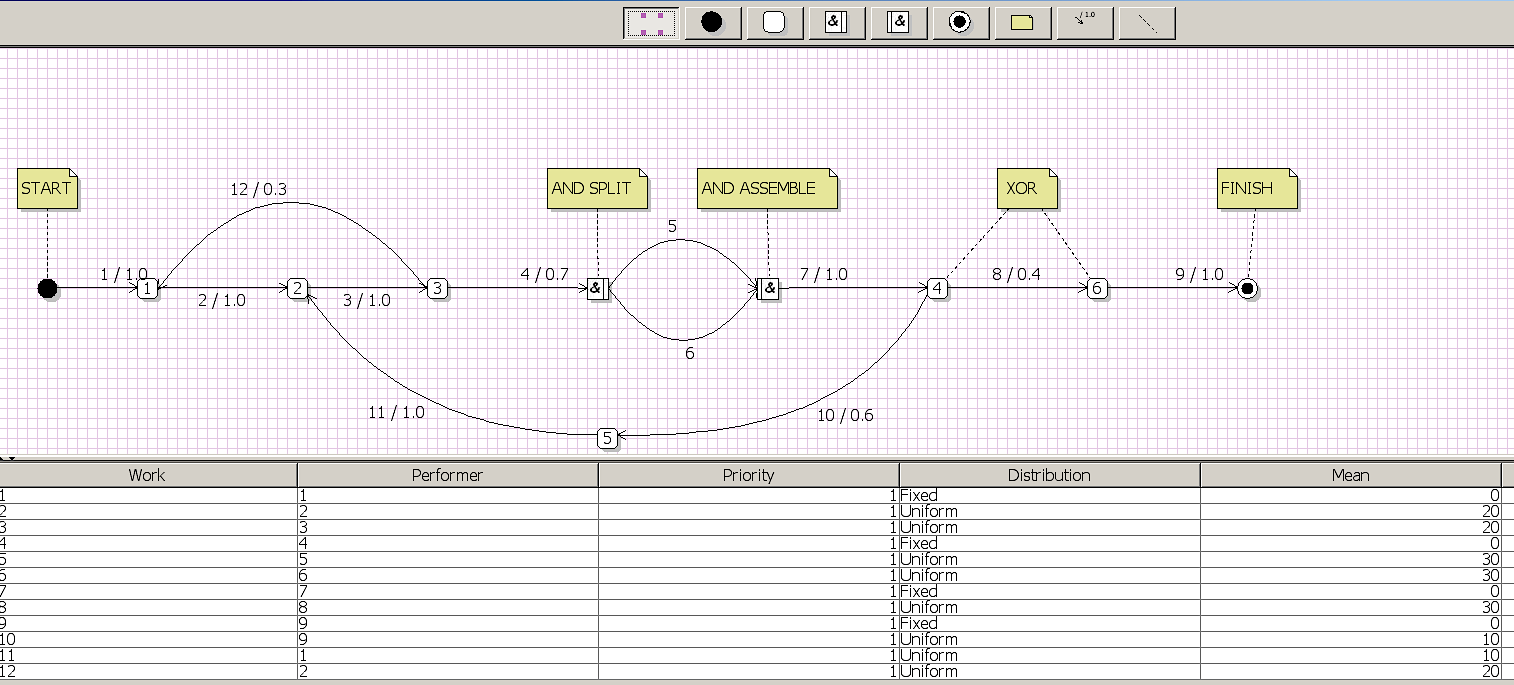
GPSS World: How to construct the business process simulation model executable file

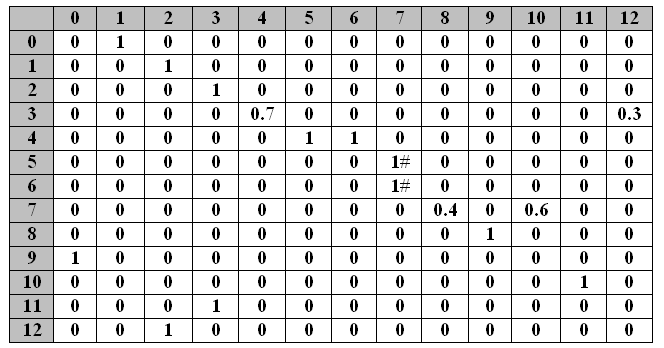
The GPSS system is best suited for the queuing networks simulation. For any business process that is represented by a probabilistic graph or a transmission matrix, the GPSS simulation program code can be generated as a custom template consisting of a limited number of segments. Moreover, the text of a significant part of the segments remains unchanged, no matter how the structure and parameters of the business process change. The structure of the template program remains invariant with respect to the quantitative and qualitative parameters of the simulated business process. This is the point of using a single GPSS template for a business process simulation program. The expressive power of the GPSS system allows the routing of claims using a set of FUNCTION commands, each of which practically displays the corresponding row of the transmission matrix P . FUNCTION commands are also used to define the activity duration distributions. The GPSS code of the business process modelling program is presented in the APPENDIX. Two program fragments are highlighted with bold: the one containing a set of FUNCTION commands that provide routing of claims in accordance with the probabilistic graph (Figure 01 ) and the one that determines the functioning of the queuing network node. The invariance of the last fragment with respect to the structure of the business process is provided by the use of the transaction parameters. The program Violet-BP, which provides automatic code generation GPSS-business process modelling program on its probabilistic graph is created by Dmitry Korenev on the concept and algorithm of the author. Program Violet-BP is written in Java based on an open framework of the Violet diagrams editor. Figure 1 shows a screen shot of the main application window. Figure 03 shows a histogram of the business process duration in question as the result of data processing obtained for 5000 experiments with the simulation model. After importing simulation results from GPSS World, a histogram and empirical distribution function are constructed, and then compared with the corresponding approximations obtained analytically (Sidnev, 2016) by three goodness of fit tests: Kolmogorov-Smirnov, Pearson (Chi-square), Kramer-Mises-Smirnov (omega-square) at the significance level α = 0.05. The final choice between the null and alternative hypotheses is made by the majority principle. Figure 03 shows analytical PDF compared with the empirical one created by simulation. The Hypothesis H₀ is accepted by all three goodness of fit tests. Thus, the correctness of the generated GPSS-model of the business process is confirmed.

See Full Size >

The executable file formation in the environment of modeling systems focused on the use of Petri nets formalism

The number of modeling packages using Petri nets, which are mentioned in various sources, clearly exceeded one hundred. Note also that the idea to use the Petri net formalism for queuing networks modelling is not new (Mutarraf, Barkaoui, Li, Wu & Qu, 2018) and is implemented, in particular, in the QPME package (Queuing Petri net Modelling Environment) (Al-Azzoni, 2017). It is proposed to consider the implementation of the proposed approach in relation to the simulation packages Mobius and CPN Tools, focused on the use of extended Petri nets. The structure of the Petri net is known to be given by a pair of matrices D^- and D⁺ whose strings are the input and output transition functions of the Petri net.

The transmission matrix of queuing network is easily transformed into the mentioned pair of matrices. Figure 04 shows the matrix D^- and D⁺, corresponding to the transmission matrix of the single-channel queuing network shown in Figure 02 .

See Full Size >

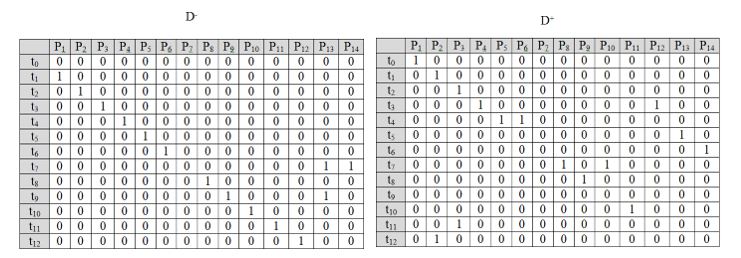
The executable file of the CPN Tools simulation model has a cpn extension and is an xml file. The structure of the cpn file is open. The contents of the file can be modified with an external program by modifying, adding, removing lines of code, thereby determining the appropriate changes to the Petri net. Mobius (Keefe & Sanders, 2015) package involves the use of Stochastic Activity Networks formalism, which is an extended Petri nets. The object model in this case consists of three files with different extensions. Two of them are service files that are almost invariant to the content of the simulated object. The third file with the cpp extension is a C# code that is available for analysis and can be generated by an external program. Thus, the Petri net constructed from the initial representation of the probabilistic graph of the business process can be transformed into formalisms used by the CPN Tools and Mobius packages.

Findings

1. The proposed concept of business process modeling is fundamentally feasible.

2. The proposed concept has been brought to practical implementation in relation to the GPSS World simulation system — the Violet-BP business process model editor has been developed to automatically generate the GPSS program code.

3. The study of a number of modeling systems, namely, CPN Tools, Mobius, Anylogic, based on the use of different formalisms allows us to conclude that this modeling concept is applicable to them

Conclusion

The number of different simulation systems is increasing at high speed. This circumstance is primarily due to the emergence of new objects to be simulated and the need to obtain a tool especially designed for the new object simulation.

An alternative concept is to use well-known and reputed simulation systems together with specially developed software-editors that automatically generate the code of the object simulation program for some class of objects. The proposed concept of business process modeling can be developed in different directions and extended to any modeling objects.

APPENDIX: GPSS MODEL CODE

Generated by Violet-BP 0.1a

alpha EQU 3 ; order of Erlang distribution

GENERATE_TIMING VARIABLE (Exponential(1,0,130000))

T_IME TABLE M1,0,30,40

DISTRIB_Fixed VARIABLE (FN$M_EAN)

DISTRIB_Uniform VARIABLE (Uniform(2,(0.4#FN$M_EAN),(1.6#FN$M_EAN)))

DISTRIB_Exponential VARIABLE (Exponential(1,0,FN$M_EAN))

DISTRIB_Triangular VARIABLE (Triangular(3,(0.4#FN$M_EAN),(1.6#FN$M_EAN),FN$M_EAN))

DISTRIB_Erlang VARIABLE (Gamma(3,0,(FN$M_EAN/alpha),alpha))

; Performers:

; 1 => 1

; 2 => 2

; 3 => 3

; 4 => 4

; 5 => 5

; 6 => 6

; 7 => 7

; 8 => 8

; 9 => 9

;

; Works:

; 1 => 1, 1001

; 2 => 2, 1002

; 3 => 3, 1003

; 4 => 4, 1004

; 7 => 5, 1005

; 8 => 6, 1006

; 9 => 7, 1007

; 10 => 8, 1008

; 11 => 9, 1009

; 12 => 10, 1010

; 5 => 11, 1011 #

; 6 => 12, 1012 #

NODE_NUM FUNCTION P$COLNUM,D12

1,1/2,2/3,3/4,4/5,7/6,8/7,9/8,9/9,1/10,2/11,5/12,6

P_RIORITY FUNCTION P$COLNUM,D12

1,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9,1/10,1/11,1/12,1

M_EAN FUNCTION P$COLNUM,D12

1,0.0/2,20.0/3,20.0/4,0.0/5,0.0/6,30.0/7,0.0/8,10.0/9,10.0/10,20.0/11,30.0/12,30.0

D_ISTRIBUTION FUNCTION P$COLNUM,D12

1,0/2,2/3,2/4,0/5,0/6,2/7,0/8,2/9,2/10,2/11,2/12,2

A_DVANCE ADVANCE V$DISTRIB_Fixed

TRANSFER ,R_ELEASE

ADVANCE V$DISTRIB_Uniform

TRANSFER ,R_ELEASE

; Transfer matrix:

GRID EQU 10

MAXCOLNUM EQU 12

LINE_0 FUNCTION RN1,D13 ; generate

0.0,0/1.0,1/1.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_1 FUNCTION RN1,D13 ; 1

0.0,0/0.0,1/1.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_2 FUNCTION RN1,D13 ; 2

0.0,0/0.0,1/0.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_3 FUNCTION RN1,D13 ; 3

0.0,0/0.0,1/0.0,2/0.0,3/0.7,4/0.7,5/0.7,6/0.7,7/0.7,8/0.7,9/1.0,10/1.0,11/1.0,12

LINE_4 FUNCTION RN1,D13 ; 4

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/0.0,5/0.0,6/0.0,7/0.0,8/0.0,9/0.0,10/0.0,11/1.0,155 ; ->11 ->12

LINE_5 FUNCTION RN1,D13 ; 7

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/0.0,5/0.4,6/0.4,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_6 FUNCTION RN1,D13 ; 8

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/0.0,5/0.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_7 FUNCTION RN1,D13 ; 9

1.0,0/1.0,1/1.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_8 FUNCTION RN1,D13 ; 10

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/0.0,5/0.0,6/0.0,7/0.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_9 FUNCTION RN1,D13 ; 11

0.0,0/0.0,1/0.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_10 FUNCTION RN1,D13 ; 12

0.0,0/0.0,1/1.0,2/1.0,3/1.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_11 FUNCTION RN1,D13 ; 5

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

LINE_12 FUNCTION RN1,D13 ; 6

0.0,0/0.0,1/0.0,2/0.0,3/0.0,4/1.0,5/1.0,6/1.0,7/1.0,8/1.0,9/1.0,10/1.0,11/1.0,12

ASSMB_OFF FUNCTION P$COLNUM,D3

10,1/11,0/12,0

A_SSEMBLE ASSEMBLE 2

TRANSFER ,M_OVE

GENERATE V$GENERATE_TIMING

ROW_0 ASSIGN COLNUM,FN$LINE_0

TRANSFER ,SERV

ROW_1 ASSIGN COLNUM,FN$LINE_1

TRANSFER ,SERV

ROW_2 ASSIGN COLNUM,FN$LINE_2

TRANSFER ,SERV

ROW_3 ASSIGN COLNUM,FN$LINE_3

TRANSFER ,SERV

ROW_4 ASSIGN COLNUM,FN$LINE_4

TRANSFER ,SERV

ROW_5 ASSIGN COLNUM,FN$LINE_5

TRANSFER ,SERV

ROW_6 ASSIGN COLNUM,FN$LINE_6

TRANSFER ,SERV

ROW_7 ASSIGN COLNUM,FN$LINE_7

TRANSFER ,SERV

ROW_8 ASSIGN COLNUM,FN$LINE_8

TRANSFER ,SERV

ROW_9 ASSIGN COLNUM,FN$LINE_9

TRANSFER ,SERV

ROW_10 ASSIGN COLNUM,FN$LINE_10

TRANSFER ,SERV

ROW_11 ASSIGN COLNUM,FN$LINE_11

TRANSFER ,SERV

ROW_12 ASSIGN COLNUM,FN$LINE_12

TRANSFER ,SERV

SERV TEST NE P$COLNUM,0,FIN

TEST G P$COLNUM,MAXCOLNUM,S_TART

S_PLIT SAVEVALUE COLNUM_1,((P$COLNUM-P$COLNUM@(MAXCOLNUM+1))/(MAXCOLNUM+1))

SAVEVALUE COLNUM_2,(P$COLNUM@(MAXCOLNUM+1))

SPLIT 1,CHILD

ASSIGN COLNUM,X$COLNUM_1

TRANSFER ,S_TART

CHILD ASSIGN COLNUM,X$COLNUM_2

TRANSFER ,S_TART

S_TART PRIORITY FN$P_RIORITY

QUEUE (P$COLNUM+1000)

QUEUE P$COLNUM

SEIZE FN$NODE_NUM

DEPART P$COLNUM

TRANSFER FN,D_ISTRIBUTION,A_DVANCE

R_ELEASE RELEASE FN$NODE_NUM

DEPART (P$COLNUM+1000)

TEST GE P$COLNUM,GRID,M_OVE

TRANSFER FN,ASSMB_OFF,A_SSEMBLE

M_OVE SAVEVALUE ROOTER,(P$COLNUM#2)

ASSIGN ROOTER,X$ROOTER

TRANSFER P,ROOTER,ROW_0

FIN TABULATE T_IME

References

1. Al-Azzoni, I. (2017). ATL Transformation of Queueing Networks to Queueing Petri Nets. In L. F. Pires, S. Hammoudi and B. Selic (Eds), Proceedings of the 5th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2017) (pp. 261-268), Porto, Portugal: Scitepress.
2. Artamonov, I. V. (2018). Osobennosti primeneniya algoritmicheskogo podhoda k modelirovaniyu biznes-processov [Features of application of the algorithmic approach to modelling business processes]. Vestnik Altajskoj akademii ekonomiki i prava, 2, 5-11. [in Rus].
3. Babkin, Е. A., & Kopica, Е. V. (2016). O metodologii imitacionnogo modelirovaniya biznes-processov na osnove agentnogo I diskretno-sobytijnogo podhodov [On the methodology of simulation modeling of business processes bazed on agent-bazed and discrete-event approaches]. Auditorium, 2(10). 72-77. [in Rus]
4. Boubeta-Puig, J., Diaz, G., & Macia, H. (2019). MEdit4CEP-CPN: An approach for complex event processing modeling by prioritized colored petri nets. Information systems, 81, 267-289.
5. Gradišar, D., & Mušič, G. (2012). Automated Petri-Net Modelling for Batch Production Scheduling. In P. Pawlewski (Ed.) Petri Nets. Manufacturing and Computer Science (pp. 3-26). London; InTech.
6. Jensen, K., & Kristensen, M. (2009). Colored Petri Nets. Modelling and Validation of Concurrent Systems. Berlin: Springer-Verlag Berlin Heidelberg. doi:
7. Kanduč, T., & Blaž, R. (2015). Automated simulation model building for a complex furniture manufacturing process. Retrieved from https://www.researchgate.net/publication/303425362_ Manufacturing_processes_optimisation_in_a_furniture_factory
8. Keefe, K., & Sanders, W. H. (2015). Reliability Analysis with Dynamic Reliability Block Diagrams in the Möbius Modeling Tool. In W. Knottenbelt, K. Wolter, A. Busic, M. Gribaudo & P. Reinecke (Eds.), Proceedings of the 9th EAI International Conference on Performance Evaluation Methodologies and Tools (VALUETOOLS), (pp. 164-170). Berlin, Germany: ICST.
9. Lapina, L. A., Stupina, A. A., Kiryakova, O. V., Kapustina, S. V., Voloshin, R. V., & Gron', D. N. (2015). O podhodah k vyboru instrumentariya modelirivaniya biznes-processov [Aproaches to the selection of tools for business process modelling]. Sovremennye problemy nauki i obrazovaniya, 2(2), 57. [in Rus].
10. Mutarraf, U., Barkaoui, K., Li, Z., Wu, N., & Qu, T. (2018). Transformation of Business Process Model and Notation models onto Petri nets and their analysis. Advances in mechanical engineering, 10(12), 168781401880817. https://doi.org/10.1177/1687814018808170
11. Nastyuk, A. V., Kulikova, Е. S., Trubina, G. F., & Nazarov, A. D. (2017). Anylogic kak instrument imitacionnogo modelirovaniya biznes-processov kompanii [Anylogic as simulation tool the business processes of the company] Moskovskij ekonomicheskij zhurnal, 3, 10. [in Rus].
12. Safiullin, A. R., Devyatkov, T. V., & Zakirova, E. A. (2015). Podhod k razrabotke effectivnoj sistemy obsluzhivaniya na osnove modelirovaniya biznes-processov [The approach to developing an effective service system based on simulation modeling of business processes]. Kazanskij ekonomicheskij vestnik. 6(20), 94-101. [In Rus].
13. Sidnev, A. (2016). The essence of the mathematical business process models discipline for computer science students. In L. G. Chova, Al. Martinez & I. C. Torres (Eds), ICERI2016 Proceedings (pp. 8236-8242). Seville, Spain: IATED. doi:
14. YAkimov, I. M., Kirpichnikov, A. P., Mokshin, V. V., Alyautdinova, G. R., & Pajgina, L. R. (2015). Imitacionnoe modelirovanie biznes-processov v sisteme Bizagi Modeler [Simulation modelling of business processes in Bizagi Modeler]. Vestnik Tekhnologicheskogo universiteta, 18(9), 236-239. [in Rus].
15. Zaharov, V. N. (2016). Insrtumenty modelirovaiya biznes-processov [Business process modelling tools]. Vestnik Moskovskogo gosudarstvennogo oblastnogo universiteta. Seriya: Ekonomika, 3, 48-53. [in Rus].