The Complexity of The Mathematics Education Within Early Education Conceptual field

Abstract

Starting from the kindergarten to the university level, among of the education vital roles which must be fulfilled, such as the development of constructively and critically thinking students, the empowerment of citizenship towards the creation of a better society, generation of awareness of issues of equality and justice, this has to promote the vital fact that in a society there are “responsibilities” as well as “rights”. Not in the last, a better society is based on the technological progress which are accomplished through the sciences and mathematics knowledge. In this framework, the education brings its major role for the society within the school environment by formatting the students for that they will become the future engineers, teachers, doctors, economics, etc. for a future society. The goal of our paper is to analyse the professional development of the teachers for the kindergarten (educators) and primary school (teachers) in the context of the current reforms in science education from the perspective of teachers’ mathematics knowledge. At least in our country, in the international framework of the reform efforts for the STEM goals have often been unsuccessful because they failed because those teachers' knowledge, beliefs, and attitudes that should to consider. But do academics and university professors have no essential role in building the pre-university education system? Is this an issue that we should submit to an education research? Who has the scientific and honorary responsibilities to answer these questions?

Keywords: Mathematics educationscholar programsprofessional competencesteaching mathematics

Introduction

The title of our paper intentionally contains four, more or less new, keywords or syntagma that are highly circulated and manipulated in the education research domains: complexity, early education, mathematics didactics, conceptual field. If we were to develop each these terms from the point of epistemological, of historical, of application domains them or of their contextual semantics that are used today within educational domains; then we could write whole books. It is not our intention! But we have to delineate some important ideas for them. Thus, when mathematicians use the words “complex” and “complexity” they think either at a dynamic system governed by a nonlinear differential-integral equation or at a problem from the chaos theory (Broer & Takens, 2011; Hirsch, Smale, & Devaney, 2004) or at a simple algebraic second-degree equation. Mathematicians often use the word nonlinearity instead of complexity. By “dynamic system”, mathematicians understand a set of nonlinear autonomous differential equations that are “expressing” in mathematical language the interactions between the parts of a physical, biological, engineering, social, etc. system. The more the real system within a particular science which studies on him is better known, i.e. it is correctly and complexity described in the “language” of that science, the faster and better it can associate in the mathematical language a mathematics dynamic system for him. About this “idea” were written books, treatises, etc. In the last five decades, the interest of researchers from the almost all scientific domains have increased for the use of Complex Dynamic Systems Theory within their own research field, even if some of them have introduced changes or new “interpretations”, which are more or less a bit far away from the facilities offered by mathematics, such as General System Theory (von Bertalanffy, 1968), Systemic Dynamics (Forrester, 1968), etc.

As expected, and in the scientific domain of education, the theory of dynamic systems has been “imported” (Davis, & Sumara, 2008; Jacobson, & Wilensky, 2006; Levin, & Jacobson, 2017; Trombly, 2014) with a more or less suited understanding of it, so that some confusions or misunderstanding occurred. The last two inconveniences mentioned previous arise, for example, when attempting to get a “isomorphism” for the didactic interaction between the teacher and his class of students with a “network communication” in which teaching and learning activities are “blended”, and approaching is without the mathematics fundaments. By the other hand, it is very difficult to make such a scientific foundation through mathematics because social systems, in general, an education system, in particular, are hard to specify by their real properties of existence and uniqueness. It is obviously that these are widely variety.

We have tried to give a dimension of the link between education and the theory of dynamic systems (Nicolescu & Petrescu, 2013), but to advance in this direction we should have a fair and open interdisciplinary and/or transdisciplinary collaboration between mathematics researchers and education researchers. It is very interestingly that the researchers in the domain of education prefer to approach to the neural sciences to explain the teaching and learning processes within educational systems (National Research Council, 2000; National Academies of Sciences, Engineering, and Medicine, 2018). Probably the time will come when the sciences of education will accept as research partners also mathematicians, physicists, chemists, engineers, etc. for a real development of the knowledge of the “world”. This is a good starting point for education research domain, as a "whole subsystem", within the knowledge-based society which has adopted "the holistic approach of the knowledge" as an important axiom of its.

Not by „hazard”, the title of the paper contains, by juxtaposition, even two new concepts imposed by the new directions of current research in the field of education, each with different sources of emergence and “asymptotic development” in this domain: “early education” and “conceptual field”. The World Conference “Education for All”, Jomtien (Thailand) 1990, is considered as the “initial” starting point of the “big bang” for the early education concept. A new perspective brought by this concept has led to an “explosive” development of the theories of substantiation about the child's education processes within the kindergarten, as a first step for his lifelong learning. This “early education’s story” is so long (Silva, et al., 2015), and we believe that it isn’t finish yet. The conceptual field is a “new baby born” in the education research domain. We find a possible definition of this concept in Vegnaud (2009): “It is at the same time a set of situations and a set of concepts tied together. By this, I mean that a concept’s meaning does not come from one situation only but from a variety of situations and that, reciprocally, a situation cannot be analysed with one concept alone, but rather with several concepts, forming systems." Is this definition embedded in the complex systems theory or is a new one? This just a rhetoric question!

In this complex frame of the theories concerning all above concept, we try to define the position and role of the mathematics education inside the early education through the teachers’ knowledge of the mathematics teaching in the kindergarten, which are acquired by them through learning about mathematics, mathematics education, and by pedagogical practice in our university program Pedagogy of the Primary and Preschool Education (PPPE).

Without losing our common sense, we did ask many times ourselves by why it is so "complex" our didactic interactions (in sense of research in mathematics education at university level) with our students (i.e. adults) on the issues of mathematical activities for pre-schoolers. We have always projected our course's theoretical discourse for the students based on the general ideas that have been shown true over all history of mankind: mathematics is a language for description of the real world (Hansen, & Gray, 2010); mathematics has its important role in our everyday life (Hodaňová, & Nocar, 2016); through their own experiences on things, interactions, phenomena, etc. from their immediate environment etc. After a rich and long-lasting experience in teaching "didactics of kindergarten math activities" within the PPPE program, we can say that it is a complex activity that is very little talked about in the field of academic research at the university level. In other words, we have studied the mathematics education from the many different points of view (Bagni, Furinghetti, & Spagnolo, 2004; Bagni, 2004; Björklund, 2015).

Problem Statement

In this complex frame of the theories concerning all above concept, we try to define the position and role of the mathematics education inside the early education through the teachers’ knowledge of the mathematics teaching in the kindergarten, which are acquired by them through learning about mathematics, mathematics education, and by pedagogical practice in our licence program “Pedagogy of the Primary and Preschool Education” (PPPE).

The holism “translated” in the sense of education led, among other things, to the integrated design of the curriculum for the preschool and for the primary school curricula. For example, for the first three primary classes, holism involved the emergence of a new discipline “Mathematics and Environmental Exploration” for which the issue of this discipline’s didactics has not been seriously addressed. The integrated design of all activities at pre-school level remains another set of issues at the teachers’ training level. What should can university professors do to overcome these new issues within the teacher training program? After all, even university professors have to solve the real problems of society! However, even we though mathematics that the education has reached a first stage of maturity, it is definitely not marked by coherence and unity, let alone uniformity, but rather by considerable complexity and diversification in perspectives and paradigms. Against this background it is not a trivial matter for a single individual to set out to identify and discuss key issues and trends in research on mathematics education (Niss, 2004).

As far as we know, even today, there has been no attempt for a real research in the teaching and learning mathematics education for bachelor programs other than those of mathematics department. This is quite the case with the PPPE program. What would such new research bring? Well, first of all university professors should know how to teach mathematics for some of their students who have ceased to learn mathematics since these had 16 years old, because they had chosen to go on a humanist trajectory at the high school. In addition, their attitude towards mathematics is characterized by a “fear of mathematics”, by “a rejection” of mathematics, by the feelings of “mathematics’ uselessness”, etc. The students of this kind have difficulty learning and understanding even for the issues of mathematics education for pupils from the kindergarten and from the primary school. Yet these students will become educators or teachers, and for the us remain the rhetorical question: How will they respond to their future students' needs such as them learning mathematics needs and expectations?

Research Questions

The university professors really know what are the needs and expectations of the national primary and pre-school education system? This question is putting and for us too! For find out the true answer in our case, we ask for a collaboration to our students that together get starting a research about it. So, our research was started first with the direct discussions with our students within the university course and seminar of “Didactics of the Mathematics Activities in the Kindergarten”. First, we were interested in the what way we are able to formed our students for that they will become the good educators for their kindergarten pupils. We can say that our statically group consists of our students from the undergraduate program of “Pedagogy of the Primary and Preschool Education”, from the subsidiaries of the University of Pitesti, i.e. Slatina, Alexandria and Pitesti, during of the three years of study in the academic years 2014-2017, in total 540 students. We always ask our self if our students will be able to project really activities in which the mathematical knowledge will be ensuring so such the pupils will can describe their “known world” also in “the mathematics language”. This is an issue for us when we conduct some of the specified mathematics education knowledge from curriculum requirements for early education. In short, are we as teachers fully useful to our students for their future profession of educator? Do we respect the following dialectic rapport: the research influences the practice of teaching mathematics in the pre-university education system and, reciprocally, the practice of teaching mathematics in the pre-university education system is a “sit” for the investigation for the research?

Purpose of the Study

Throughout the entire PPPE program, we have worked with this group of students across several courses. Thus, from the first year to the end of the program, these courses were: Mathematics for Preschool, Mathematics for Primary, Arithmetic, Didactics of Mathematics Activities in Kindergarten, Didactics of Mathematics for Primary Education, Information and Communication Technology. In all teaching activities related with these university courses and seminars, we have come to a state of frank and open collaboration with our students based on the didactic contract. In other words, we as teachers have tried to meet the expectations and needs of our students in order to form professional competencies related to school curriculum programs that contain the requirements for the framework objectives in the field of science (kindergarten) and the general competencies for the disciplines Mathematics and environmental exploration and Mathematics (primary cycle).In the last year, i.e. 2017, we tried to measure the quality of our performance in relation to our students based on a questionnaire developed by us. From the outset, we have to say that this study does not have the power of a generalization or an important cover for research in the field of education. The purpose of this study is simply an attempt to establish a "strategy" on which we as teachers „learn” how to teach our students how to become teachers who will be able to teach mathematics knowledge at primary level and preschool.

As far as we know, even today, there has been no attempt for a real research in the teaching and learning mathematics education for bachelor programs other than those of mathematics department. This is quite the case with the PPPE program. What would such new research bring? Well, first of all university professors should know how to teach mathematics for some of their students who have ceased to learn mathematics since these had 16 years old, because they had chosen to go on a humanist trajectory at the high school. In addition, their attitude towards mathematics is characterized by a “fear of mathematics”, by “a rejection” of mathematics, the feelings of “mathematics’ uselessness”, etc. The students of this kind have difficulty learning and understanding even for the issues of mathematics education for pupils from the kindergarten and from the primary school. Yet these students will become educators or teachers, and for the us remain the rhetorical question: How will they respond to their future students’ needs such as them will learning mathematics?

Research Methods

The following questions which we are selecting from the questioner of us inquire for the purpose of the study are:

• Do you think that you have always recognized, during the practice-time (in the mentoring activity), patterns, theories or templates learned at the courses in your study program?

• Yes

• No

• I do not know.

• To what extent did you use your acquired knowledge during „Pedagogy of Education for Primary School and Preschool” program within your activities of the pedagogical practice?

• To a great extent

• To a large extent

• To a small extent

• Not at all

• I do not know

3.To what extent are you satisfied (in the sense that you understood) of the concepts of didactics of mathematics (early education) related to what you really need to do with your future students in the classroom?

• Total dissatisfied

• Partially satisfied

• Satisfied

• Very satisfied

We have limiting ourselves to analysing only these three questions from our questionnaire given to students, because the idea of this paper is to highlight the interdependence between how university professors believe to prepare teachers for primary and preschool education and the real states of the teaching and learning mathematics in the education system according to school curricula. This has to be done in the real time. A source to find out the true about this issue is to ask for our students to tell us what do they think about we do for them? They can compare between the what the know from reality during the pedagogical practice and what they actually learning from us.

Findings

The answers to these three questions were statistically processed and the results obtained are given below in Tables 01 , and the graphical representations of these results in Fig. 01 .

See Full Size >

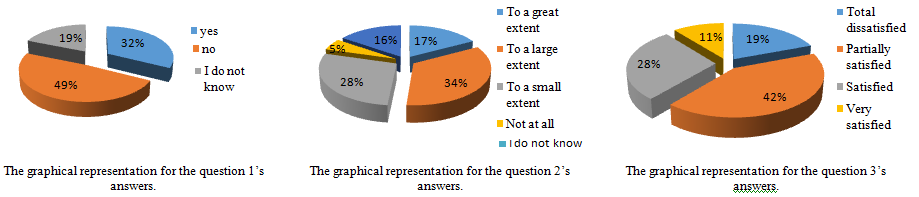
Although the answer to this question was the negative one, we believe it is because of the form or structure of certain courses, where the student makes it harder to link the scientific notion presented and the actual content to be taught in the preschool or primary cycle. Of course, most of the times when we discussed the conceptual function, we were told that this concept is beyond the preschool and primary cycle, and that only in the 8th grade is discussing the function. This is a false idea because the students forget the link between “academics knowledge” and the “knowledge for teaching” from the mathematics curriculums for the preschool and primary cycle.

In the second question, the answers of the students are more favourable because after the discussions at the courses or seminars, there were also analysing discussions on the evaluating for their semesterly works (projects, portfolios, etc.). Within these discussions we justified and argued for each student in part how we evaluate his products. Moreover, the student has practically “corrected” his own work together with us. We have adopted this way to conduct assessment exams so that each student understands during the exam where or what he / she did not know or did not learn. Thus, the student learns to evaluate and evaluate himself.

Although these diagrams can be interpreted differently according to what we want to see, although the answers of our students were on average for a good score, we can only declare ourselves partially satisfied. We have to admit that we could have done more for our students if they were more committed to critical learning activities. But speaking of complexity, we can say there are a lot of disturbing factors for the teacher-student system that do not lead to very good results. This is not a “trick” to apologize us.

The analysis of the results presented above shows us that, at least globally, the perception of our students regarding the acquisition of scientific knowledge and the formation of their professional skills are good. It is obvious that their expectations have not been fully met. At least, from our point of view, we accept this reality. The complexity of designing and realizing a teacher training plan is in itself a complex process and, unfortunately, connecting him to society's needs is a long-time relationship to the evolution dynamics of the society.

Conclusion

One of the fundamental ideas which do not have to forget is the fact that mathematics education had reached the point where research and practice could work together in productive dialectic. In the case of early education mathematics there are and other big ideas:

• mathematics for the child must be a bridge between him and future world (Anthony, & Walshaw, 2009);

• mathematics is hidden in things, music, painting, ballet, sports, etc.;

• the child can find out all about mathematics through everything he/she does;

• the child is the most important “dynamical system” of the early education (Härkönen, 2002), etc.

Last but not least, the university professors which teaching mathematics and its didactics for PPPE program should learn how to communicate all their academic knowledge in these scientific fields in a sustainable way to students coming from high school curricula where mathematics discipline has very few hours allocated or simply disappears from the curriculum. Otherwise, for these students it can be considered that nothing has been done to train them as teachers for primary school and kindergarten. And this will have serious consequences in the future!

The story of early education and mathematics for this stage of children's education is very beautiful when we think of “child” only as an “angelic concept” that we must “love it”. It is wrong approaching for the child in this way! Let us look at him carefully, to teach him that we know how to approach him, to ask him what he dreams of about he/she will want to do in his/hers future, etc. But do not forget that a good practice must fulfil following true: “Good mathematics pedagogy can be enacted when educators engage children in a variety of mathematically-related activities across different areas of learning. The activities should arise from children’s interests, questions, concerns and everyday experiences” (NCCA, 2014, p. 9). On the other hand, we are proposing to: “The premises and importance of early-school and school education are supported by the latest results of psychology, pedagogy, etc. that highlight early learning fostering learning opportunities later on. Early acquired skills and knowledge fosters the development of others later, and deficiencies in knowledge and skills lead to longer-term deficiencies, poorly exploited learning opportunities” (Tudor, 2015, p. 4). How can we harmonize, melt, assemble these two basic ideas of the theory of early education? Do we know to accomplish the child's spectrum and this is may be like a unique “pattern”? What are the “monads” (Leibniz, 1965) of the child's spectrum? At least until now, we can ask whether the monads can be written as follows: “The educational aims formulated in the school curriculum for the different levels of education are supported by formal, non-formal and in-formal education. For early education, educational aims, defined in terms of competences in the school curricula aims: training the child's personality, respecting his level of development; equipping the child with the knowledge, skills and attitudes that boost the creative and effective reporting on social and natural environment allowing further education” (Tudor, 2016).

Russell (1952, p. 6) believed that the three ingredients that changed the science outlook of the eighteenth century were:

• Statements of the fact should be based on observation, not on unsupported authority.

• The inanimate world is a self-acting, self-perpetuating system, in which all changes conform to natural laws.

• The earth is not the centre of the universe, and probably Man is not its purpose (if any); moreover “purpose” is a concept which is scientifically useless.

Starting from these, we think that is time to elaborate the theories in the early education based on the observations about what child is and does. He/she is a self-acting, self-perpetuating system, and his/her is changing conform to his/her natural laws which we just we are just looking to understand them. The Child is the centre of the early education ...., and not vice-verse! For all these we need more practice in communication in any knowledge' domains with our children within or out of school. In our opines, all the early educational theories become valid if the child’s dreams will be fulfilled. For that the educator has to say: “Quiet! The Child is deeming! We must follow his dreams!” (Fig. 02.).

See Full Size >

References

1. Anthony, G., & Walshaw, M. (2009). Mathematics Education in the Early years: building bridges. Contemporary Issues in Early Childhood 10(2), 107-121. DOI:
2. Bagni, G. T., Furinghetti, F., & Spagnolo, F. (2004). History and epistemology in mathematics education. In L. Cannizzaro, A. Pesci & O. Robutti (Eds.), Research and Teacher Training in Mathematics Education in Italy: 2000-2003, 207-221. Milano: Ghisetti, & Corvi.
3. Bagni, G. T. (2004). History of Mathematics and Didactics: reflections on teachers’ education. Retrieved from http://www.syllogismos.it/history/Icme10-DG6.pdf
4. Björklund, C. (2015). Pre-primary school teachers’ approaches to mathematics education in Finland. Journal of Early Childhood Education Research 4(2), 69-92.
5. Broer, H. W., & Takens, F. (2011). Dynamical Systems and Chaos, Appl. Math. Sci., vol. 172. New York: Springer.
6. Davis, B. & Sumara, D. (2008). Complexity as a theory of education. Transnational. Curriculum Inquiry 5(2). Retrieved from http://nitinat.library.ubc.ca/ojs/index.php/tci
7. Forrester, J. W. (1968). Principles of Systems. Cambridge, Massachusetts: MIT Press.
8. Hansen, A.L., & Gray, J.J. (Eds.) (2010). History of Mathematics. In Encyclopaedia of Life Support Systems (EOLSS), Vol.1. Oxford: Eolss Publishers. Retrieved from http://www.eolss.net/ebooklib/
9. Härkönen, U. (2002). Defining Early Childhood Education Through Systems Theory. Retrieved from https://www.researchgate.net/publication/228876062
10. Hirsch, M.W., Smale, S., & Devaney, R. L. (2004). Differential Equations, Dynamical Systems, and an Introduction to Chaos. New York: Academic Press of Elsevier.
11. Hodaňová, J., & Nocar, D. (2016). Mathematics importance in our life. In L. Gómez Chova, A. López Martínez, & I. Candel Torres (Eds.) INTED 2016 Proceedings 10th International Technology, education and Development Conference, March 7th -9th 2016, Valencia, Spain, 3086-3092. Valencia: IATED Academy.
12. Jacobson, M. J., & Wilensky, U. (2006). Complex System in education: Scientific and Educational importance and Implications for the Learning Sciences. The Journal of the Learning Sciences, 15(1), 11-34.
13. Leibniz, G.W. (1965). Monadology, and Other Philosophical Essays. Indianapolis: Bobbs-Merrill Co.
14. Levin, J.A., & Jacobson, M. J. (2017). Education as a Complex System: implications for Educational Research and Policy. Retrieved from https://www.researchgate.net/publication/312938036
15. National Academies of Sciences, Engineering, and Medicine (2018). How People Learn II: Learners, Contexts, and Cultures. Washington, DC: The National Academies Press. Retrieved from
16. National Research Council (2000). How People Learn: Brain, Mind, Experience, and School: Expanded Edition. Washington, DC: The National Academies Press. Retrieved from
17. NCCA (2014). Mathematics in Early Childhood and Primary Education (3-8 years). Teaching and Learning. Dublin: National Council for Curriculum and Assessment
18. Nicolescu, B. N. & Petrescu, T. C. (2013). Dynamical Systems Theory – A Powerful Tool in the Educational Sciences. Procedia–Social and Behavioral Sciences, 76(15), 581-587. DOI:
19. Niss, M. (2004). Key Issues and Trends in Research on Mathematical Education. In H. Fujita, Y. Hashimoto, B.R. Lee, S. Lerman, & T. Sawada (Eds.) Proceedings of the Ninth International Congress on MathematicalEducation: Comprehensive Approach to Acquiring Complex FacilitiesandProjects, Tokyo/Makuhari 2000, 37-57. New York: Kluver Academic Publishers.
20. Russel, B. (1952). The impact of science on society. New York: AMS Press.
21. Silva, A. R., Brandão de Sant'anna, J., Pereira de Cabral, L.L., Soares, J.L., Silva Martins de Souza, S. E. & de França Barros, J. (2015). Educaçãoprecoce: umarevisãointegrativa de literatura. Pensar a Prática, Goiânia, 20(4), 853-862. DOI:
22. Trombly, C.E. (2014). Schools and Complexity. Complicity: An International Journal of complexity and Education, 11(2), 40-58.
23. Tudor, S. L. (2016). The role of non-formal and informal education in competences training - transversal competences. In Proceedings of the 8th ECAI - International Conference of Electronics, Computers and Artificial Intelligence, 30 June -02 July, 2016, Ploiesti, România.
24. Tudor, S. L. (2015). Educația la vârsta timpurie și școlară mică în contextul instruirii centrate pe competente. Craiova: Sitech.
25. Vegnaud, G. (2009). The Theory of conceptual Fields. Human development, 52, 83-94.
26. von Bertalanffy, L. (1968). General System Theory. New York: George Braziller.