Play in Scientific and Mathematical Non-Formal Education. Bagh Chal, a Tigers-and-Goats Game

Abstract

This work introduces the Playful Projects-based methodology, created with the aim of contributing to scientific and mathematic literacy from the STEM education perspective by means of work plans designed around traditional world board games. This methodology adapts that of Ethnomathematical Projects to non-formal educational contexts, building upon games as sociocultural objects of interest and play as a learning facilitator. Here, a summary of the first Playful Project designed around the Nepali board game bagh chal is presented. This is a bipersonal, zero-sum, complete and perfect information game. This Playful Project will be implemented in two middle schools in Granada, Spain. Students will learn the game and acquire certain knowledge about it by formulating hypotheses, validating or refuting them, making deductions, and drawing conclusions. In addition to the development of the characteristic skills of STEM disciplines, our proposal is meant to foster interculturality, inclusion, and playful as well as dialogic learning.

Keywords: Scientific educationmathematical educationSTEM educationplayful learningworld board gamesnon-formal education

1.Introduction

Here, we interpret scientific, mathematical, and technological literacy within the scope of

educational action in order to achieve the maximum development and the best possible performance in

each person’s life as well as in democratic participation and citizenship. As expressed by Acevedo

(2004, pp. 12-13), this aim of scientific education “must be addressed to contributing to citizenship

education above all”.

To achieve this literacy requires facilitating scientific learning and stimulating students’ interest in

sciences (Esteban, 2003). Science contextualization proves necessary in this task, thus addressing

socially relevant scientific topics in teaching, in addition to hypothesis formulation, observation, data

interpretation, and decision making (Esteban, 2003). Sanmartí and Marchán (2015) indicate that a

scientifically competent student is a student who can reflectively engage in matters related to science

and the ideas of science. This approach influences not only which sciences and which mathematics are

to be taught, but also how these disciplines are to be taught.

Bergen (2009) considers it necessary to encourage playful behaviour and to educate through play in

order to develop STEM disciplines (sciences, technology, engineering, and mathematics) and STEM-

related skills. The underlying idea is that the enquiry and reasoning of scientists and mathematicians

resembles children’s way of thinking when playing meaningfully.

Through adequately planned educational activities, play stimulates cognitive, emotional, and

communicative development while fomenting meaningful learning, all of which are essential aspects in

the construction of social knowledge (Melo & Hernández, 2014). More specifically, formal games

(games with rules) foster important skills needed in STEM disciplines, such as: creativity; meaningful

and complex problems solving (Barab & Landa, 1997), spatial thinking (Newcombe, 2010); hypothesis

formulation and argumentation; scientific approach to answering questions and drawing scientific

conclusions (Sanmartí & Marchán, 2015); enquiry and autonomy; innovation; interpretation;

mathematical modelling and analogy.

Furthermore, scientific and mathematical education extended to the sociocultural sphere, as in non-

formal contexts such as hands-on museums, toy libraries, science clubs, fairs and workshops, is

believed to lead to long-lasting achievements. Non-formal education relieves curriculum pressure,

fostering a holistic, cross-curricular, interdisciplinary approach.

Playful activities require resources that permit the development of play idiosyncrasy. To generate

these, we advocate the use of games that can serve as educational resources in both the formal and the

non-formal context (Fernández-Oliveras & Oliveras, 2014a). More specifically, we deem the use of

traditional strategy games as particularly valuable for scientific and mathematical education in non-

formal contexts. Williford (1992, p. 98) states that these games are “attractive vehicles for enhancing

general mathematical-reasoning skills”. Precisely, an educational environment organized around games

stimulates positive attitudes towards learning among students, and facilitates cognitive achievement, as

revealed by conceptions of future teachers in training (Fernández-Oliveras & Oliveras, 2014b, 2015).

In this sense, Ferguson (1995) reported improvements in multiple scientific and mathematical thinking-

related skills through educational chess: abstract reasoning, strategic planning, evaluation and

synthesis, critical thinking, problem solving, decision making, creativity, and flexibility. Wan et al.

(2011) have shown that professional shogi players’ apparently intuitive performance comes from an

enhanced pattern-recognition skill developed by experience and deliberate practice.

Similarly, we can assume that other similar strategy games may offer comparable benefits. Two

fundamental processes take place in these games: 1) mental construction of the game tree , in which

players use short-term memory, visuospatial skills, logical relations, heuristic strategies, analogy, and

modelling; 2) best-next-move selection, where players use pattern recognition, logical relations, long-

term memory, goal-based decisions, option evaluation, and decision making.

In the words of Melo and Hernández (2014),

Recognition of play as an essential function of human knowledge evolution and development,

and therefore of education, is fundamental, as to establishing its true pedagogical value and

recognising its merits in every dimension of the individual development. (p. 42)

Non-formal contexts, which encourage active participation of students of any age, allow enquiry-

based approaches. These require dedicating long time allotments to experiencing and reflecting on

activities, which may prove difficult to find in formal schooling. Moreover, participation in

extracurricular activities stimulates personal development during adolescence and early adulthood

(Eccles & Templeton, 2002; Eccles, Barber, Stone & Hunt, 2003; Mahoney, 2000). These activities

foster both peer relationships and relationships with adults, facilitate the formation of positive identities

(Eccles et al., 2003), stir motivation and leadership (Eccles & Templeton, 2002). This is the approach

we adopt in the experience presented in this work.

2.Objectives

We consider that some zero-sum1, complete2 and perfect information3 strategy games, such as chess,

can offer comparable benefits to those derived from it (Ferguson, 1995). This is the basis of our

proposal, for which the objectives are:

General objectives: 1.Contributing to scientific and mathematical literacy in a non-formal educational context,

fostering scientific, mathematical and cross-curricular competences development through

traditional world board games-based work.

2.Fostering interculturality, inclusion and dialogue as fundamental bases for personal

relationships and scientific learning in multicultural contexts.

Specific objectives: 1.Practicing some world board games as samples of activation of scientific and mathematical

thinking implicit in specific cultural contexts.

2.Explicitly stating modelled features of scientific and mathematical thinking immerse in the

games practiced.

1 A zero-sum non-cooperative game is one in which the victory (gain) or defeat (loss) of a player equally and complementarily matches the defeat (loss) or victory (gain) of the other players.

2 A complete information game is one in which every player is aware of the rewards and strategies available to other players.

3 A perfect information game is one in which every player is aware of all previously occurred events and decisions.

3.Collecting evidence of scientific and mathematically-inspired thinking in the approach of

games by participant players.

4.Validating our approach of world board games-based educational proposal.

5.Fostering playful culture, analysing and promoting educational values inherent to practiced

games.

6.Divulging some world board games as specific cultures’ heritage reflecting on their

cosmogonies, thus developing sociocultural knowledge.

3.Methodology

The proposal is structured around the teaching methodology of Ethnomathematical Microprojects

created by Oliveras (2005, 2008). Microprojects are open interdisciplinary work plans, designed

around a sociocultural object of interest, seeking the active and responsible participation of students in

the construction of interdisciplinary contextualized meanings, especially regarding scientific and

mathematical learning, and promoting a truly intercultural education. We have adapted this

methodology to the study of games as ethnomathematical sociocultural objects, creating what we here

term Playful Projects.

These Playful Projects are sequences of learning, communication, and reflective action activities

constructed around a game, and they encompass a wide variety of sociocultural, scientific, and

mathematical aspects. They are specially addressed to non-formal educational contexts. From a games

theory perspective, the games considered are bipersonal, zero-sum, complete and perfect information

games; from a cultural anthropology standpoint, they are world strategy board games.

An enquiry experience will be conducted in two educational centres in Granada, Spain, during the

third trimester of the academic course 2015-2016 to pursue the objectives stated above.

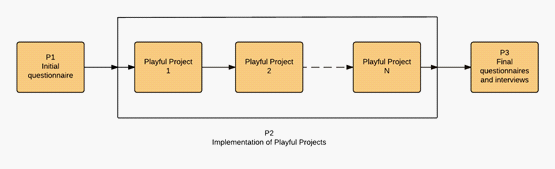
As shown in Figure 1 , this experience is divided into three phases. Phase 1, initial semi-structured

questionnaire, is meant to assess personal playful and gaming background of participants as well as

playful environment provided in their educational centre. In phase 2, Playful Projects are implemented,

with participant observation and discussion groups. Finally, in Phase 3, questionnaires are administered

to analyse: development of scientific and mathematical thinking as well as other cross-curricular skills

(semi-structured), level of satisfaction, planning, and general development of the experience.

Optionally conducted interviews aim to further deepen insights.

See Full Size >

Within Phase 2, Playful Projects follow a structure begun with the study of the game under

consideration as an ethnomathematical sociocultural object, from which specific aspects relevant to

STEM education emerge. This study is conducted in accordance with three categories taken from

Huxley’s (1955) concept of culture: artifact, mentifact, and socifact. Activities specifically designed

around the game to encourage scientific and mathematical thinking follow, presented in teaching

itineraries corresponding to the participants’ educational level.

Playful Projects are conducted in one-hour sessions in which the research team encourages player

enquiries, registers relevant observations, and makes audiovisual recordings.

In this work, we summarize the first Playful Projects to be implemented, entitled “Bagh Chal, a

Tigers-and-Goats Game”. The game bagh chal was selected from a previously prepared list of games of

interest (Gutiérrez-Perera, Fernández-Oliveras & Oliveras, 2015) for its potential in scientific and

mathematical education.

4.Playful Project “Bagh Chal, a Tigers-and-Goats Game”

4.1.The game-artifact. Modelling game components

See Full Size >

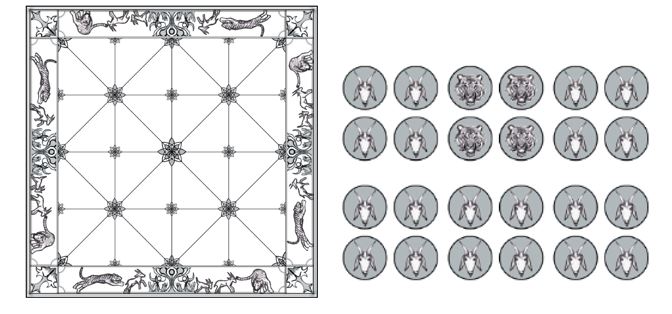
The game takes place on a square board ( Figure 2 , a) with 24 pieces, 20 of which represent goats and the remaining 4 represent tigers ( Figure 2 , b).

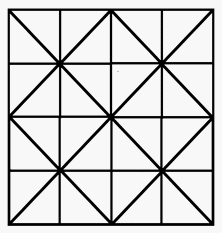
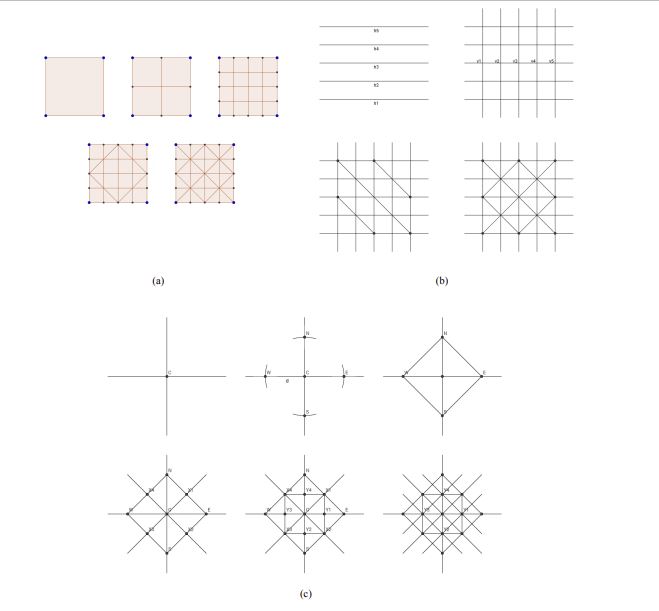
4.1.1. Geometric characterization and construction of the board

The board is formed by two groups of parallel lines – five horizontals and five verticals, intersecting

in a 5x5 point grid, and six diagonal lines as shown in Figure 3 . The pieces are positioned at the

intersection points during the game, and not at the triangular areas delimited by lines.

See Full Size >

Figure 4 shows three distinct procedures for constructing the board, all of which can be completed

freehand, using a straightedge and compass, or with software such as GeoGebra. Due to space

restrictions, we cannot include the algorithmic descriptions of the constructions.

4.1.2. Technological construction of the pieces and the board

The abstract nature of the game is manifested in the fact that it is traditionally played on boards

excavated or drawn on the ground, using pebbles, little sticks or cattle excrement for pieces.

Manufactured boards are usually made of brass or wood, with a size of between 20 and 30 cm per side,

and pieces tend to be made of brass, wood, resin or plastic.

Any set of pieces can be used, provided that players agree upon its representation. The 20 pieces

representing goats must be equal to one another, and different from the 4 pieces representing tigers,

which in turn must be equal to one another. Shape is not important, as the game can be played in an

abstract fashion, as long as the size of the pieces is adequate in relation to that of the board and the

hands of the players, and the pieces have a flat side which can lie on the board. We suggest using

recycled or waste materials (e.g. caps, corks, clothes-pegs), beans, chickpeas, coins or coloured pieces

of glass. If figurative pieces are preferred, we recommend making these out of handicraft materials

such as clay, modelling clay, air-dried plaster, recycled paper, etc.

See Full Size >

4.2.The game-mentifact. Game classification, rules, strategies

4.2.1. Game classification

According to mathematical games theory (Leyton-Brown & Shoham, 2008; Shoham & Leyton-

Brown, 2010), bagh chal is a bipersonal (it involves two players), finite (regarding the number of

available strategies or choices), dynamic (players do not simultaneously decide their strategies),

sequential (players alternate turns), non-cooperative (players compete and cannot win or lose together),

zero-sum, complete and perfect information game.

According to Ballesteros (2005), whose classification is based on the game objective and the type of

strategy employed to pursue it, bagh chal belongs to the family of tafl games, since it involves two

unequal opposing forces which try to capture the other player’s pieces.

Other authors (Gutiérrez-Perera, 2014, p.33), considering the symbolic aspects, classify it as a

hunting game, since it involves a confrontation between animal predators and prey, which is

idiosyncratic of the game’s cultural context. The two forces have “different objectives and even

different movement rules”: specifically, prey cannot capture, a distinctive factor in contrast to war

games, in which both forces can capture the opponent’s pieces.

4.2.2. Game rules

One player controls four tigers, initially placed on the board corners. The other player controls 20

goats, initially placed outside of the board. For the tigers, the objective is to capture five goats, while

the goats must completely block all of the tigers’ legal moves. The goats start the game.

The game takes place in two different phases. During the first phase, goats are placed, one per turn,

on any free intersection point; they cannot be moved. Tigers move, one per turn, to a free adjacent

intersection point along a line. A tiger can capture an adjacent goat if it can jump over it onto a free

intersection point on the other side, as long as the three points (origin, goat-occupied, and destination)

are aligned and interconnected. A tiger cannot jump over two goats, change jump direction in mid-air,

or make more than one capture in one turn. Capturing is not mandatory.

Figure 5 shows one possible opening sequence from the game start, up to the conclusion of the

fourth turn. See a goat being captured in the tigers’ second turn, after a forced mistake made possible

by a poor initial placement on the goats’ side. However, on their third turn, the tigers miss a capture

opportunity, allowing the goats to strengthen their position on the fourth turn.

See Full Size >

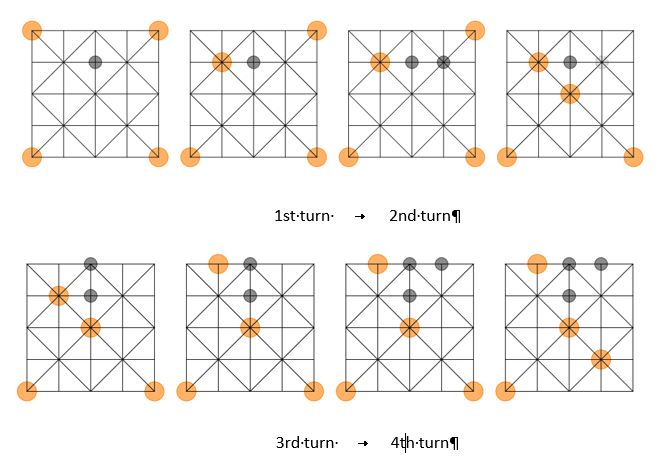
During the second phase, which starts once the 20 goats have been placed into the board, goats can

start moving, one per turn, to a free adjacent intersection along a line. They cannot capture tigers.

Tigers’ movement and capture rules are the same in both phases.

4.2.3. Regarding strategy and tactics

Bagh chal is not as widely popular and studied as chess is, this limiting information about possible

winning or facilitating strategies. “The placement phase involves a search whose game-tree complexity

is estimated to be of the order 1041”, according to Lim and Nievergelt (2004, p. 131). Ignoring

symmetric variants, the number of possible positions during the placement phase is 6,633,059,000,

while during the movement phase, it is 88,260,972 (Lim & Nievergelt, 2004). Size and structure of the

state space significantly delayed the game’s computational analysis, even though it was finally

determined that when played optimally on both sides bagh chal ends in a draw (Lim & Nievergelt,

2009).

Figure 6 shows the five possible opening moves for the goats. Any other choice is analogous to one

of these five, due to the symmetry of the game board. Options (a) and (b) in the figure expose the goat,

offering an immediate capture. Option (d) allows the tigers to force a capture in their second turn, as

sequence on Figure 5 shows. Option (e) gives optimally playing tigers the possibility to force an early

capture, which should occur at most in their fifth turn, since in their fourth turn they can make a move

that is called “scissors” in chess, a double-threat so that the defender can save only one of the exposed

goats with the other one being inevitably captured. Option (c) is the only one which allows goats to

start a solid cantonment and avoid an early capture. Hence, the goats’ first move is practically

mandatory among those available if they are not willing to make an early sacrifice.

See Full Size >

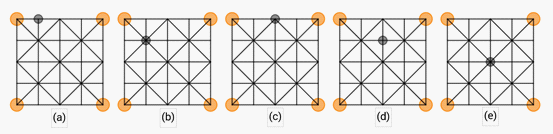
A facilitating strategy for the goats during the placement phase is to occupy the board sides and

corners. During the movement phase, there is one simple principle: the goats must try to advance in

unison in order to trap the tigers. They can manage to do so if they get to introduce free points into the

herd space, rendering them inaccessible to the tigers via jumps; in this way, they effectively control

available space and can hold it so that it is not returned into dispute, considerably reducing the tigers’

mobility.

Optimally playing tigers can force the capture of at least two goats during the placement phase.

Nevertheless, if they do not take this advantage and that phase ends with only one free point, the game

becomes complicated for them due to the mobility reduction. In that situation the goat herd can

frequently maintain a closed formation long enough to corral the tigers. During the movement phase

the tigers have little choice but to wait for the goats’ mistakes (sub-optimal decisions), thus limiting

tiger choices to tactical aspects. For the tigers, two fundamental goals at any moment are looking for

scissor-like moves and keeping as scattered on the board as possible, thus threatening more space for

plausible captures and trying to avoid being blocked all at once.

4.3.The game-socifact. Sociocultural aspects of the game

The game’s name bagh chal (��� ��� bāgh cāl , in Nepali language, ��� ���� dhun kasa , in

Newar or Nepal Bhasa) can be translated as “the tiger moves” or “the tiger’s movement”. The tiger is

commonly considered king of the animals in Asia and therefore has a leading role in several games

from East and Southeast Asia which represent the tiger’s hunt of different prey.

Bagh chal is Nepal national game and said to be “ideal to play when the summer mornings’ sun is

too strong”. Nepali tradition says the game was created by Mandodari ( Figure 7 ), daughter of

Mayasura, King of the Asuras , and Hema, apsara water nymph. Mandodari (“soft-bellied”) is Queen

consort of Ravana, King of Lanka, according to the Hindu epic Ramayana, and belongs to the

Panchakanya , a group of five maidens the recital of whose names is believed to dispel sin.

4.4.STEM aspects of interest

With this Playful Projects, educators can work on the following STEM aspects with students-

participants:

- - Pieces involved: characterization, identification, count; representation of the abstraction.

- Board abstract geometry: 1. Descriptive aspects: characterization, constituent elements,

symmetry. 2. Constructive aspects: freehand, compass and straightedge, GeoGebra, other tools.

- Game tree: subset graph of the extensive-form game, representing the game development from

the start up to a given time.

- Next-move tree: subset graph of the extensive-form game, representing mental forecast of the

game development from a given time, showing several possible sequences of future moves.

- Abstract codification systems: to annotate game development representing moves in a coded

record of the game-tree nodes actually traversed.

- Argumentation.

- Deductive reasoning.

- Spatial thinking: 1. Orientation: localization and description of moves in a plane, cardinal

points, technological tools (compass or GPS). 2. Representation: Cartesian axes and

coordinates, floor plan, relation to maps and scales.

- Predation: biological interaction in ecosystems. Predators and prey. Food chain and trophic

levels.

- Natural environment: impact on cultural idiosyncrasies. Geographical, climatological, and

natural characterization of the origin.

- - Predator-prey mathematical model: Lotka-Volterra’s equations.

- Technological aspects: 1. Material selection: usage of recycled materials; reason and

convenience; practical, economic and ecologic considerations. 2. Construction of board and

pieces: tool selection, size choice, construction execution.

- Artistic aspects: design, craft, and decoration of board and pieces.

See Full Size >

5.Conclusions

This work introduces a methodology based on Playful Projects as an adaptation of

Ethnomathematical Microprojects. These Playful Projects are open interdisciplinary teaching modules,

constructed around a world board game interpreted as a sociocultural and ethnomathematical object of

interest. They are specifically designed to contribute to scientific and mathematical education in non-

formal contexts. Playful Projects, implemented via series of one-hour sessions, encompass sequences

of learning, communication, and reflective action activities, which are meant to motivate participants

and foster scientific and mathematical thinking as well as enquiry.

The Playful Project entitled “Bagh Chal, a Tigers-and-Goats Game”, based on Nepali traditional

game bagh chal, is presented. This game represents a confrontation between two asymmetrical forces

in a hunt scenario. The Playful Project has been designed to work on several relevant aspects from a

STEM educational perspective, such as spatial thinking and orientation, geometric modelling, strategy,

deductive reasoning, representation, coding, analogy, scientific speech, biological interactions.

We propose this as a pertinent and enriching approach to scientific and mathematical education

through world-games-based proposals, firstly, because play is a teaching resource proven to activate

emotional and cognitive factors, thus fostering the development of multiple skills; and secondly,

because these games are samples of cultural scientific and mathematical thinking (Bishop, 1998;

Gerdes, 1988) that can encourage intercultural and interdisciplinary education, a fundamental need in

today’s evermore globalized world.

Acknowledgements

To the Secretariado de Innovación Docente (University of Granada, Spain) for financing Teaching Innovation Project l5-44.

References

1. Acevedo, J. A. (2004). Reflexiones sobre las finalidades de la enseñanza de las ciencias: educación científica.
2. (), para la ciudadanía. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias, 1(1), 3-16.
3. Ballesteros, S. (2005). Juegos de mesa del CCS. , mundo. Madrid
4. Barab, S. A.Landa, A. (1997). Designing Effective Interdisciplinary Anchors. Educational Leadership, 54(6), 52-55
5. Bergen, D. (2009). Play as the Learning Medium for Future Scientists, Mathematicians and Engineers. American Journal of Play, 1(4), 413-428
6. Bishop, A. J. (1998). El papel de los juegos en educación matemá Revista de Didáctica de las Matemáticas. , 18, 9-19, tica. Uno
7. Eccles, J. S.Barber, B. L.Stone, M.Hunt, J. (2003). Extracurricular activities and adolescent development. Journal of Social Issues, 59(4), 865-889
8. Eccles, J. S.Templeton, J. (2002). Extracurricular and other after-school activities for of Research in Education, 113-180. , youth. Review
9. Esteban, S. (2003). La perspectiva histórica de las relaciones Ciencia-Tecnología-Sociedad y su papel en la enseñanza de las ciencias. Revista Electrónica de Enseñanza de las Ciencias, 2(3), 399-415
10. Ferguson, R. (1995). Chess in Education Research Review of Key Chess Research Studies. Paper presented at the Borough of Manhattan Community College “Chess in Education: A Wise Move” Conference, Summary. A
11. Fernández-Oliveras, A.Oliveras, M. L. (2014a). Playing for science and mathematics education: an experience for pre-service kindergarten teacher M. F. M. Costa, P. Pombo, B. V. Dorrío. , training. In
12. (), 190
13. (), eISSN: 2357-1330 Selection & Peer-review under responsibility of the Conference Organization Committee
14. (), (Eds.), Hands-on Science. Science Education with and for Society (180 -183). Braga: Hands-on Science Network. Retrieved from http://www.hsci.info/Book_HSCI_2014_ lowresA4.pdf.
15. Fernández-Oliveras, A.Oliveras, M. L. (2014b). Pre-service kindergarten teachers’ conceptions of play, science, mathematics, and education. Procedia - Social and Behavioral Sciences, 152, 856-861. DOI
16. Fernández-Oliveras, A.Oliveras, M. L. (2015). International Journal on Advances in Education Research. EduRe_V2_I1_P3.pdf. , 2(1), 37-48, Retrieved from http://edure.org/EduReJournalVol2N1/
17. Gerdes, P. (1988). On culture, geometrical thinking and mathematics education. Educational Studies in Mathematics, 19(2), 137-162
18. Gutiérrez-Perera, C. S. (2014). Programación didáctica de la asignatura de 4º de ESO Trabajo Monográfico de Investigación: "Juegos de mesa del mundo y etnomatemáticas". Unpublished master’s thesis, Universitat Jaume Castelló, Spain. Gutiérrez-Perera, C. S., Fernández-Oliveras, A., & Oliveras, M. L. (2015). Analizando y seleccionando juegos del mundo para la educación científica y matemática. ReiDoCrea, Revista electrónica de investigación y Docencia Creativa, monográfico Enseñanza y Aprendizaje de las Ciencias Experimentales y las Matemáticas, 22-27.. Retrieved from http://hdl.handle.net/10481/37111. . I,, Retrieved from http://repositori.uji.es/xmlui/handle/10234/108258
19. Huxley, J. S. (1955). Evolution, Cultural and Biological. Yearbook of Anthropology ( Chicago: University of Chicago, pp. 2-25)
20. Leyton-Brown, K.Shoham, Y. (2008). Essentials of Game Theory: A Concise Multidisciplinary Rafael, California: Morgan & Claypool. , Introduction. San
21. Lim, Y. J.Nievergelt, J. (2004). Computing Tigers and Goats, ICGA Journal. , 27(3), 31-141
22. Lim, Y. J.Nievergelt, J. (2009). Tigers and Goats is a draw, Games of No Chance : DOI. , 3, 163-176. MSRI
23. Mahoney, J. L. (2000). School extracurricular activity participation as a moderator in the development of antisocial development. , 71(2), 502-516, patterns. Child
24. Melo, M. P.Hernández, R. (2014). El juego y sus posibilidades en la enseñanza de las ciencias naturales. Innovación Educativa, 14(66), 41-63
25. Newcombe, N. S. (2010). Picture Th. (Increasing Math and Science Learning by Improving Spatial Thinking. American Educator, summer 2010, 29-35+43)
26. Oliveras, M. L. (2005). Microproyectos para la educación intercultural en Revista de Didáctica de las Matemáticas. , 11(38), 70-81, Europa. Uno
27. Oliveras, M. L. (2008). The IDMAMIM project is “Innovation in Didactics for Mathematics in Multicultural contexts, with Immigrant and Minority pupils”. ICME 11.. Monterrey, Mé Study Group 33: Mathematics education in a multilingual and multicultural environment. , xico. Topic
28. Sanmartí, N.Marchán, I. (2015). La educación científica del siglo retos y propuestas. Investigación y Ciencia, (469), 30-38, XXI
29. Shoham, Y.Leyton-Brown, K. (2010). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations [online]. , Retrieved from http://www.masfoundations.org/download.html
30. Wan, X.Nakatani, H.Ueno, K.Asamizuya, T.Cheng, K.Tanaka, K. (2011). The Neural Basis of Intuitive Best Next-Move Generation in Board Game Experts. Science, 331, 341-346
31. Williford, H. (1992). Games for Developing Mathematical Strategy. Mathematics Teacher, 85(2), 96-98